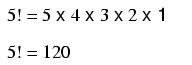
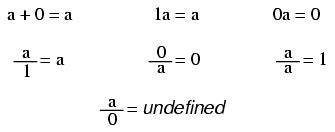
Note: while division by zero is popularly thought to be equal to infinity, this is not technically true. In some practical applications it may be helpful to think the result of such a fraction approaching infinity as the denominator approaches zero (imagine calculating current I=E/R in a circuit with resistance approaching zero -- current would approach infinity), but the actual fraction of anything divided by zero is undefined in the scope of "real" numbers.
In addition and multiplication, terms may be arbitrarily associated with each other through the use of parentheses:
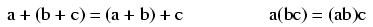
In addition and multiplication, terms may be arbitrarily interchanged, or commutated:

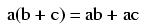
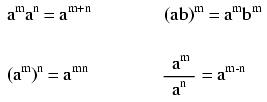
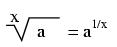
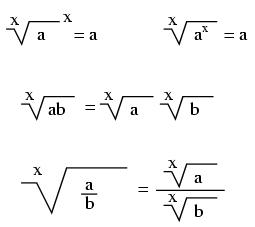
e approximately equals: 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69996
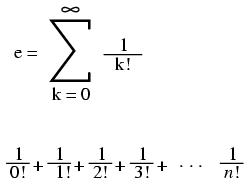
Pi approximately equals: 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37511
Pi (π) is defined as the ratio of a circle's circumference to its diameter.
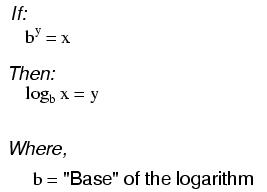
"log" denotes a common logarithm (base = 10), while "ln" denotes a natural logarithm (base = e).
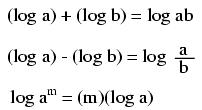
These properties of logarithms come in handy for performing complex multiplication and division operations. They are an example of something called a Transform Function, whereby one type of mathematical operation is transformed into another type of mathematical operation that is simpler to solve. Using a table of logarithm figures, one can multiply or divide numbers by adding or subtracting their logarithms, respectively. then looking up that logarithm figure in the table and seeing what the final product or quotient is.
Slide rules work on this principle of logarithms by performing multiplication and division through addition and subtraction of distances on the slide.
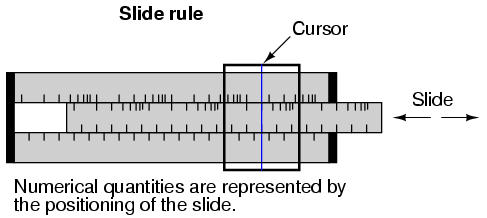
Marks on a slide rule's scales are spaced in a logarithmic fashion, so that a linear positioning of the scale or cursor results in a nonlinear indication as read on the scale(s). Adding or subtracting lengths on these logarithmic scales results in an indication equivalent to the product or quotient, respectively, of those lengths.
Most slide rules were also equipped with special scales for trigonometric functions, powers, roots, and other useful arithmetic functions.
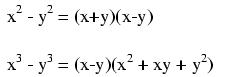



Denoted by the symbol "!" after an integer; the product of that integer and all integers in descent to 1.
Example of a factorial: