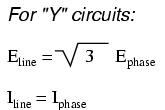




Depicted above is a very simple AC circuit. If the load resistor's power dissipation were substantial, we might call this a "power circuit" or "power system" instead of regarding it as just a regular circuit. The distinction between a "power circuit" and a "regular circuit" may seem arbitrary, but the practical concerns are definitely not.
One such concern is the size and cost of wiring necessary to deliver power from the AC source to the load. Normally, we do not give much thought to this type of concern if we're merely analyzing a circuit for the sake of learning about the laws of electricity. However, in the real world it can be a major concern. If we give the source in the above circuit a voltage value and also give power dissipation values to the two load resistors, we can determine the wiring needs for this particular circuit:
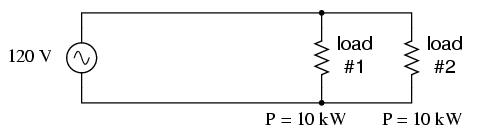

83.33 amps for each load resistor adds up to 166.66 amps total circuit current. This is no small amount of current, and would necessitate copper wire conductors of at least 1/0 gage. Such wire is well over 1/4 inch in diameter, weighing over 300 pounds per thousand feet. Bear in mind that copper is not cheap either! It would be in our best interest to find ways to minimize such costs if we were designing a power system with long conductor lengths.
One way to do this would be to increase the voltage of the power source and use loads built to dissipate 10 kW each at this higher voltage. The loads, of course, would have to have greater resistance values to dissipate the same power as before (10 kW each) at a greater voltage than before. The advantage would be less current required, permitting the use of smaller, lighter, and cheaper wire:
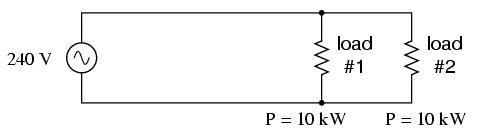
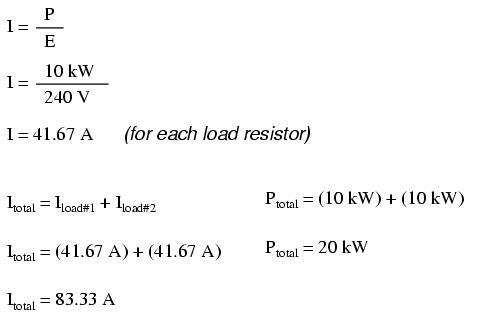
Now our total circuit current is 83.33 amps, half of what it was before. We can now use number 4 gage wire, which weighs less than half of what 1/0 gage wire does per unit length. This is a considerable reduction in system cost with no degradation in performance. This is why power distribution companies elect to transmit electric power using very high voltages (many thousands of volts): to capitalize on the savings realized by the use of smaller, lighter, cheaper wire.
However, this solution is not without disadvantages. Another practical concern with power circuits is the danger of electric shock from high voltages. Again, this is not usually the sort of thing we concentrate on while learning about the laws of electricity, but it is a very valid concern in the real world, especially when large amounts of power are being dealt with. The gain in efficiency realized by stepping up the circuit voltage presents us with increased danger of electric shock. Power distribution companies tackle this problem by stringing their power lines along high poles or towers, and insulating the lines from the supporting structures with large, porcelain insulators.
At the point of use (the electric power customer), there is still the issue of what voltage to use for powering loads. High voltage gives greater system efficiency by means of reduced conductor current, but it might not always be practical to keep power wiring out of reach at the point of use the way it can be elevated out of reach in distribution systems. This tradeoff between efficiency and danger is one that European power system designers have decided to risk, all their households and appliances operating at a nominal voltage of 240 volts instead of 120 volts as it is in North America. That is why tourists from America visiting Europe must carry small step-down transformers for their portable appliances, to step the 240 VAC (volts AC) power down to a more suitable 120 VAC.
Is there any way to realize the advantages of both increased efficiency and reduced safety hazard at the same time? One solution would be to install step-down transformers at the end-point of power use, just as the American tourist must do while in Europe. However, this would be expensive and inconvenient for anything but very small loads (where the transformers can be built cheaply) or very large loads (where the expense of thick copper wires would exceed the expense of a transformer).
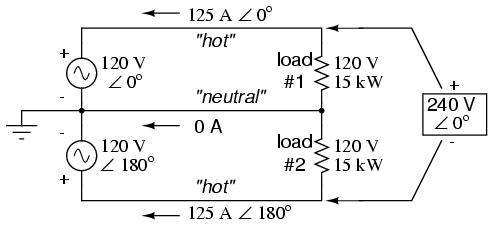
An alternative solution would be to use a higher voltage supply to provide power to two lower voltage loads in series. This approach combines the efficiency of a high-voltage system with the safety of a low-voltage system:
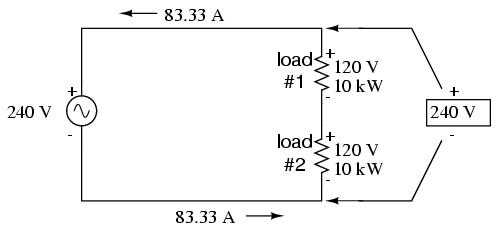
Notice the polarity markings (+ and -) for each voltage shown, as well as the unidirectional arrows for current. For the most part, I've avoided labeling "polarities" in the AC circuits we've been analyzing, even though the notation is valid to provide a frame of reference for phase. In later sections of this chapter, phase relationships will become very important, so I'm introducing this notation early on in the chapter for your familiarity.
The current through each load is the same as it was in the simple 120 volt circuit, but the currents are not additive because the loads are in series rather than parallel. The voltage across each load is only 120 volts, not 240, so the safety factor is better. Mind you, we still have a full 240 volts across the power system wires, but each load is operating at a reduced voltage. If anyone is going to get shocked, the odds are that it will be from coming into contact with the conductors of a particular load rather than from contact across the main wires of a power system.
There's only one disadvantage to this design: the consequences of one load failing open, or being turned off (assuming each load has a series on/off switch to interrupt current) are not good. Being a series circuit, if either load were to open, current would stop in the other load as well. For this reason, we need to modify the design a bit:
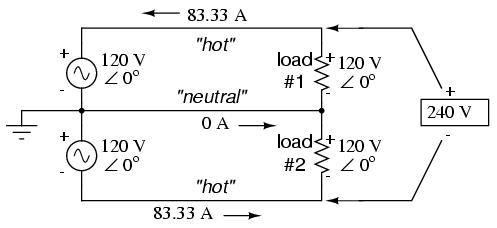

Instead of a single 240 volt power supply, we use two 120 volt supplies (in phase with each other!) in series to produce 240 volts, then run a third wire to the connection point between the loads to handle the eventuality of one load opening. This is called a split-phase power system. Three smaller wires are still cheaper than the two wires needed with the simple parallel design, so we're still ahead on efficiency. The astute observer will note that the neutral wire only has to carry the difference of current between the two loads back to the source. In the above case, with perfectly "balanced" loads consuming equal amounts of power, the neutral wire carries zero current.
Notice how the neutral wire is connected to earth ground at the power supply end. This is a common feature in power systems containing "neutral" wires, since grounding the neutral wire ensures the least possible voltage at any given time between any "hot" wire and earth ground.
An essential component to a split-phase power system is the dual AC voltage source. Fortunately, designing and building one is not difficult. Since most AC systems receive their power from a step-down transformer anyway (stepping voltage down from high distribution levels to a user-level voltage like 120 or 240), that transformer can be built with a center-tapped secondary winding:
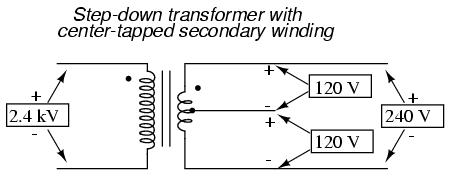
If the AC power comes directly from a generator (alternator), the coils can be similarly center-tapped for the same effect. The extra expense to include a center-tap connection in a transformer or alternator winding is minimal.
Here is where the (+) and (-) polarity markings really become important. This notation is often used to reference the phasings of multiple AC voltage sources, so it is clear whether they are aiding ("boosting") each other or opposing ("bucking") each other. If not for these polarity markings, phase relations between multiple AC sources might be very confusing. Note that the split-phase sources in the schematic (each one 120 volts ∠ 0o), with polarity marks (+) to (-) just like series-aiding batteries can alternatively be represented as such:

To mathematically calculate voltage between "hot" wires, we must subtract voltages, because their polarity marks show them to be opposed to each other:
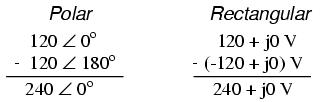
If we mark the two sources' common connection point (the neutral wire) with the same polarity mark (-), we must express their relative phase shifts as being 180o apart. Otherwise, we'd be denoting two voltage sources in direct opposition with each other, which would give 0 volts between the two "hot" conductors. Why am I taking the time to elaborate on polarity marks and phase angles? It will make more sense in the next section!
Power systems in American households and light industry are most often of the split-phase variety, providing so-called 120/240 VAC power. The term "split-phase" merely refers to the split-voltage supply in such a system. In a more general sense, this kind of AC power supply is called single phase because both voltage waveforms are in phase, or in step, with each other.
The term "single phase" is a counterpoint to another kind of power system called "polyphase" which we are about to investigate in detail. Apologies for the long introduction leading up to the title-topic of this chapter. The advantages of polyphase power systems are more obvious if one first has a good understanding of single phase systems.
Split-phase power systems achieve their high conductor efficiency and low safety risk by splitting up the total voltage into lesser parts and powering multiple loads at those lesser voltages, while drawing currents at levels typical of a full-voltage system. This technique, by the way, works just as well for DC power systems as it does for single-phase AC systems. Such systems are usually referred to as three-wire systems rather than split-phase because "phase" is a concept restricted to AC.
But we know from our experience with vectors and complex numbers that AC voltages don't always add up as we think they would if they are out of phase with each other. This principle, applied to power systems, can be put to use to make power systems with even greater conductor efficiencies and lower shock hazard than with split-phase.
Suppose that we had two sources of AC voltage connected in series just like the split-phase system we saw before, except that each voltage source was 120o out of phase with the other:
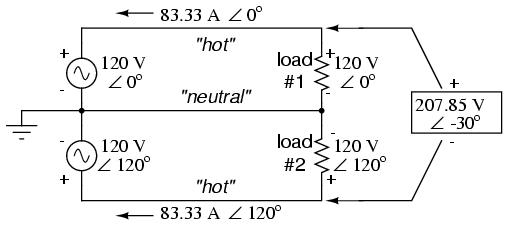
Since each voltage source is 120 volts, and each load resistor is connected directly in parallel with its respective source, the voltage across each load must be 120 volts as well. Given load currents of 83.33 amps, each load must still be dissipating 10 kilowatts of power. However, voltage between the two "hot" wires is not 240 volts (120 ∠ 0o - 120 ∠ 180o) because the phase difference between the two sources is not 180o. Instead, the voltage is:
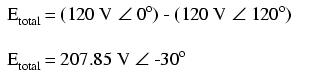
Nominally, we say that the voltage between "hot" conductors is 208 volts (rounding up), and thus the power system voltage is designated as 120/208.
If we calculate the current through the "neutral" conductor, we find that it is not zero, even with balanced load resistances. Kirchhoff's Current Law tells us that the currents entering and exiting the node between the two loads must be zero:
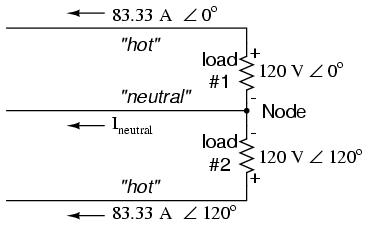
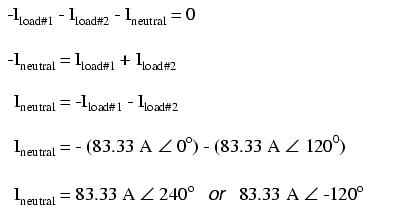
So, we find that the "neutral" wire is carrying a full 83.33 amps, just like each "hot" wire.
Note that we are still conveying 20 kW of total power to the two loads, with each load's "hot" wire carrying 83.33 amps as before. With the same amount of current through each "hot" wire, we must use the same gage copper conductors, so we haven't reduced system cost over the split-phase 120/240 system. However, we have realized a gain in safety, because the overall voltage between the two "hot" conductors is 32 volts lower than it was in the split-phase system (208 volts instead of 240 volts).
The fact that the neutral wire is carrying 83.33 amps of current raises an interesting possibility: since it's carrying current anyway, why not use that third wire as another "hot" conductor, powering another load resistor with a third 120 volt source having a phase angle of 240o? That way, we could transmit more power (another 10 kW) without having to add any more conductors. Let's see how this might look:
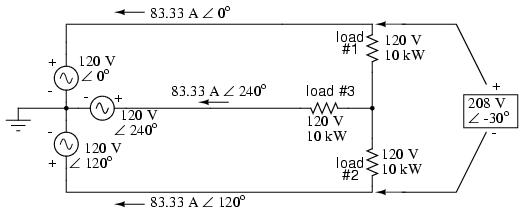
A full mathematical analysis of all the voltages and currents in this circuit would necessitate the use of a network theorem, the easiest being the Superposition Theorem. I'll spare you the long, drawn-out calculations because you should be able to intuitively understand that the three voltage sources at three different phase angles will deliver 120 volts each to a balanced triad of load resistors. For proof of this, we can use SPICE to do the math for us:
120/208 polyphase power system v1 1 0 ac 120 0 sin v2 2 0 ac 120 120 sin v3 3 0 ac 120 240 sin r1 1 4 1.44 r2 2 4 1.44 r3 3 4 1.44 .ac lin 1 60 60 .print ac v(1,4) v(2,4) v(3,4) .print ac v(1,2) v(2,3) v(3,1) .print ac i(v1) i(v2) i(v3) .end
VOLTAGE ACROSS EACH LOAD freq v(1,4) v(2,4) v(3,4) 6.000E+01 1.200E+02 1.200E+02 1.200E+02
VOLTAGE BETWEEN "HOT" CONDUCTORS freq v(1,2) v(2,3) v(3,1) 6.000E+01 2.078E+02 2.078E+02 2.078E+02
CURRENT THROUGH EACH VOLTAGE SOURCE freq i(v1) i(v2) i(v3) 6.000E+01 8.333E+01 8.333E+01 8.333E+01
Sure enough, we get 120 volts across each load resistor, with (approximately) 208 volts between any two "hot" conductors and conductor currents equal to 83.33 amps. At that current and voltage, each load will be dissipating 10 kW of power. Notice that this circuit has no "neutral" conductor to ensure stable voltage to all loads if one should open. What we have here is a situation similar to our split-phase power circuit with no "neutral" conductor: if one load should happen to fail open, the voltage drops across the remaining load(s) will change. To ensure load voltage stability in the even of another load opening, we need a neutral wire to connect the source node and load node together:
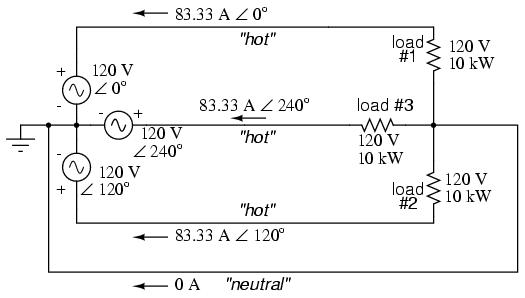
So long as the loads remain balanced (equal resistance, equal currents), the neutral wire will not have to carry any current at all. It is there just in case one or more load resistors should fail open (or be shut off through a disconnecting switch).
This circuit we've been analyzing with three voltage sources is called a polyphase circuit. The prefix "poly" simply means "more than one," as in "polytheism" (belief in more than one deity), "polygamy" (marriage to more than one wife), polyandry (marriage to more than one husband), and "polymath" (a master of more than one area of study). Since the voltage sources are all at different phase angles (in this case, three different phase angles), this is a "polyphase" circuit. More specifically, it is a three-phase circuit, the kind used predominantly in large power distribution systems.
Let's survey the advantages of a three-phase power system over a single-phase system of equivalent load voltage and power capacity. A single-phase system with three loads connected directly in parallel would have a very high total current (83.33 times 3, or 250 amps:
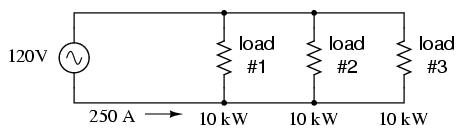
This would necessitate 3/0 gage copper wire (very large!), at about 510 pounds per thousand feet, and with a considerable price tag attached. If the distance from source to load was 1000 feet, we would need over a half-ton of copper wire to do the job. On the other hand, we could build a split-phase system with two 15 kW, 120 volt loads:
Our current is half of what it was with the simple parallel circuit, which is a great improvement. We could get away with using number 2 gage copper wire at a total mass of about 600 pounds, figuring about 200 pounds per thousand feet with three runs of 1000 feet each between source and loads. However, we also have to consider the increased safety hazard of having 240 volts present in the system, even though each load only receives 120 volts. Overall, there is greater potential for dangerous electric shock to occur.
When we contrast these two examples against our three-phase system, the advantages are quite clear. First, the conductor currents are quite a bit less (83.33 amps versus 125 or 250 amps), permitting the use of much thinner and lighter wire. We can use number 4 gage wire at about 125 pounds per thousand feet, which will total 500 pounds (four runs of 1000 feet each) for our example circuit. This represents a significant cost savings over the split-phase system, with the additional benefit that the maximum voltage in the system is lower (208 versus 240).
One question remains to be answered: how in the world do we get three AC voltage sources whose phase angles are exactly 120o apart? Obviously we can't center-tap a transformer or alternator winding like we did in the split-phase system, since that can only give us voltage waveforms that are either in phase or 180o out of phase. Perhaps we could figure out some way to use capacitors and inductors to create phase shifts of 120o, but then those phase shifts would depend on the phase angles of our load impedances as well (substituting a capacitive or inductive load for a resistive load would change everything!).
The best way to get the phase shifts we're looking for is to generate it at the source: construct the AC generator (alternator) providing the power in such a way that the rotating magnetic field passes by three sets of wire windings, each set spaced 120o apart around the circumference of the machine:
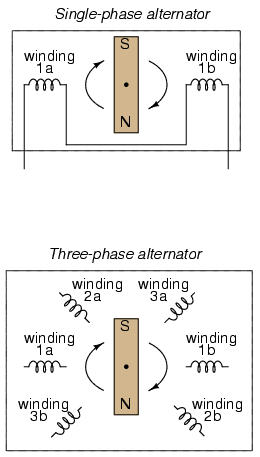
Together, the six "pole" windings of a three-phase alternator are connected to comprise three winding pairs, each pair producing AC voltage with a phase angle 120o shifted from either of the other two winding pairs. The interconnections between pairs of windings (as shown for the single-phase alternator: the jumper wire between windings 1a and 1b) have been omitted from the three-phase alternator drawing for simplicity.
In our example circuit, we showed the three voltage sources connected together in a "Y" configuration (sometimes called the "star" configuration), with one lead of each source tied to a common point (the node where we attached the "neutral" conductor). The common way to depict this connection scheme is to draw the windings in the shape of a "Y" like this:
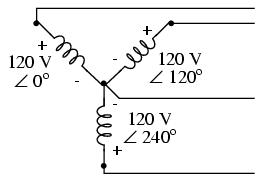
The "Y" configuration is not the only option open to us, but it is probably the easiest to understand at first. More to come on this subject later in the chapter.
Let's take the three-phase alternator design laid out earlier and watch what happens as the magnet rotates:
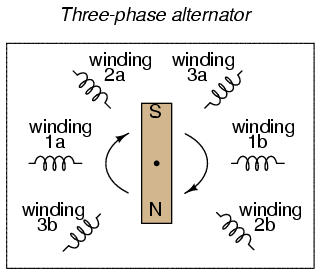
The phase angle shift of 120o is a function of the actual rotational angle shift of the three pairs of windings. If the magnet is rotating clockwise, winding 3 will generate its peak instantaneous voltage exactly 120o (of alternator shaft rotation) after winding 2, which will hits its peak 120o after winding 1. The magnet passes by each pole pair at different positions in the rotational movement of the shaft. Where we decide to place the windings will dictate the amount of phase shift between the windings' AC voltage waveforms. If we make winding 1 our "reference" voltage source for phase angle (0o), then winding 2 will have a phase angle of -120o (120o lagging, or 240o leading) and winding 3 an angle of -240o (or 120o leading).
This sequence of phase shifts has a definite order. For clockwise rotation of the shaft, the order is 1-2-3 (winding 1 peaks first, them winding 2, then winding 3). This order keeps repeating itself as long as we continue to rotate the alternator's shaft:
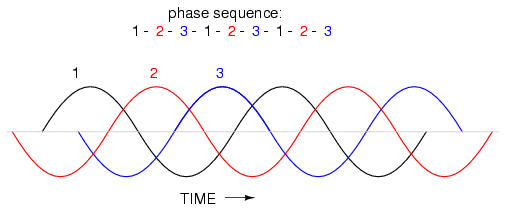
However, if we reverse the rotation of the alternator's shaft (turn it counter-clockwise), the magnet will pass by the pole pairs in the opposite sequence. Instead of 1-2-3, we'll have 3-2-1. Now, winding 2's waveform will be leading 120o ahead of 1 instead of lagging, and 3 will be another 120o ahead of 2:
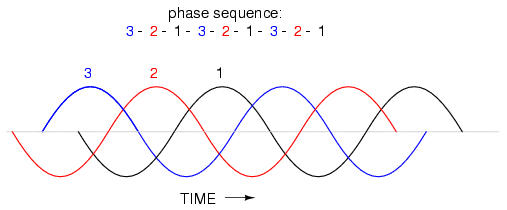
The order of voltage waveform sequences in a polyphase system is called phase rotation or phase sequence. If we're using a polyphase voltage source to power resistive loads, phase rotation will make no difference at all. Whether 1-2-3 or 3-2-1, the voltage and current magnitudes will all be the same. There are some applications of three-phase power, as we will see shortly, that depend on having phase rotation being one way or the other. Since voltmeters and ammeters would be useless in telling us what the phase rotation of an operating power system is, we need to have some other kind of instrument capable of doing the job.
One ingenious circuit design uses a capacitor to introduce a phase shift between voltage and current, which is then used to detect the sequence by way of comparison between the brightness of two indicator lamps:
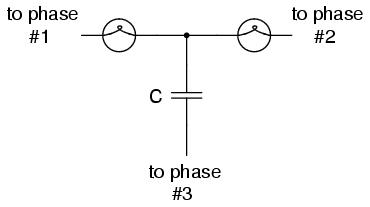
The two lamps are of equal filament resistance and wattage. The capacitor is sized to have approximately the same amount of reactance at system frequency as each lamp's resistance. If the capacitor were to be replaced by a resistor of equal value to the lamps' resistance, the two lamps would glow at equal brightness, the circuit being balanced. However, the capacitor introduces a phase shift between voltage and current in the third leg of the circuit equal to 90o. This phase shift, greater than 0o but less than 120o, skews the voltage and current values across the two lamps according to their phase shifts relative to phase 3. The following SPICE analysis demonstrates what will happen:

phase rotation detector -- sequence = v1-v2-v3 v1 1 0 ac 120 0 sin v2 2 0 ac 120 120 sin v3 3 0 ac 120 240 sin r1 1 4 2650 r2 2 4 2650 c1 3 4 1u .ac lin 1 60 60 .print ac v(1,4) v(2,4) v(3,4) .end
freq v(1,4) v(2,4) v(3,4) 6.000E+01 4.810E+01 1.795E+02 1.610E+02
The resulting phase shift from the capacitor causes the voltage across phase 1 lamp (between nodes 1 and 4) to fall to 48.1 volts and the voltage across phase 2 lamp (between nodes 2 and 4) to rise to 179.5 volts, making the first lamp dim and the second lamp bright. Just the opposite will happen if the phase sequence is reversed:
phase rotation detector -- sequence = v3-v2-v1 v1 1 0 ac 120 240 sin v2 2 0 ac 120 120 sin v3 3 0 ac 120 0 sin r1 1 4 2650 r2 2 4 2650 c1 3 4 1u .ac lin 1 60 60 .print ac v(1,4) v(2,4) v(3,4) .end
freq v(1,4) v(2,4) v(3,4) 6.000E+01 1.795E+02 4.810E+01 1.610E+02
Here, the first lamp receives 179.5 volts while the second receives only 48.1 volts.
We've investigated how phase rotation is produced (the order in which pole pairs get passed by the alternator's rotating magnet) and how it can be changed by reversing the alternator's shaft rotation. However, reversal of the alternator's shaft rotation is not usually an option open to an end-user of electrical power supplied by a nationwide grid ("the" alternator actually being the combined total of all alternators in all power plants feeding the grid). There is a much easier way to reverse phase sequence than reversing alternator rotation: just exchange any two of the three "hot" wires going to a three-phase load.
This trick makes more sense if we take another look at a running phase sequence of a three-phase voltage source:
1-2-3 rotation: 1-2-3-1-2-3-1-2-3-1-2-3-1-2-3 . . . 3-2-1 rotation: 3-2-1-3-2-1-3-2-1-3-2-1-3-2-1 . . .
What is commonly designated as a "1-2-3" phase rotation could just as well be called "2-3-1" or "3-1-2," going from left to right in the number string above. Likewise, the opposite rotation (3-2-1) could just as easily be called "2-1-3" or "1-3-2."
Starting out with a phase rotation of 3-2-1, we can try all the possibilities for swapping any two of the wires at a time and see what happens to the resulting sequence:
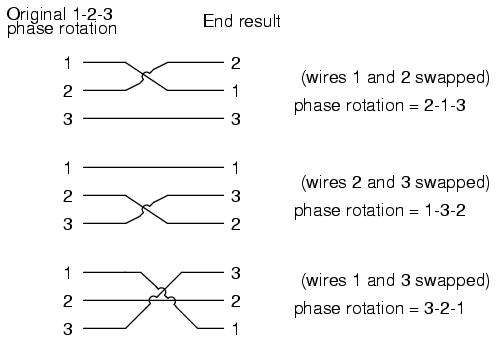
No matter which pair of "hot" wires out of the three we choose to swap, the phase rotation ends up being reversed (1-2-3 gets changed to 2-1-3, 1-3-2 or 3-2-1, all equivalent).
Perhaps the most important benefit of polyphase AC power over single-phase is the design and operation of AC motors. As we studied in the first chapter of this book, some types of AC motors are virtually identical in construction to their alternator (generator) counterparts, consisting of stationary wire windings and a rotating magnet assembly. (Other AC motor designs are not quite this simple, but we will leave those details to another lesson).
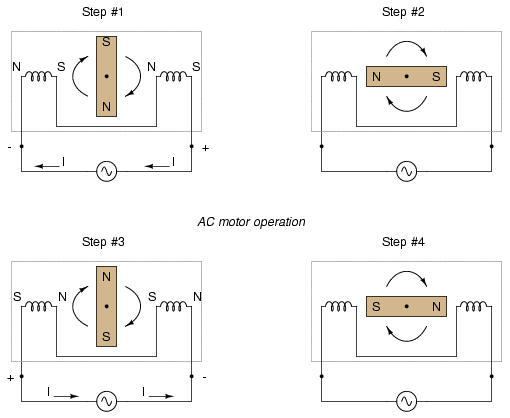
If the rotating magnet is able to keep up with the frequency of the alternating current energizing the electromagnet windings (coils), it will continue to be pulled around clockwise. However, clockwise is not the only valid direction for this motor's shaft to spin. It could just as easily be powered in a counter-clockwise direction by the same AC voltage waveform:
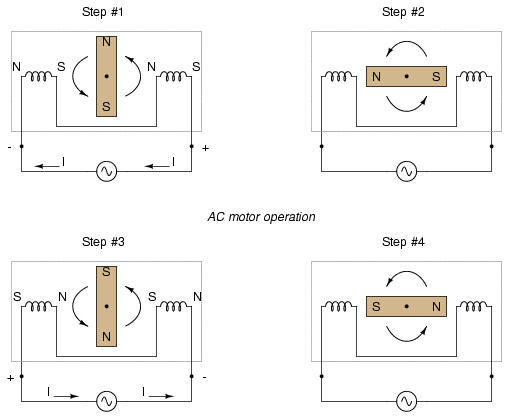
Notice that with the exact same sequence of polarity cycles (voltage, current, and magnetic poles produced by the coils), the magnetic rotor can spin in either direction. This is a common trait of all single-phase AC "induction" and "synchronous" motors: they have no normal or "correct" direction of rotation. The natural question should arise at this point: how can the motor get started in the intended direction if it can run either way just as well? The answer is that these motors need a little help getting started. Once helped to spin in a particular direction. they will continue to spin that way as long as AC power is maintained to the windings.
Where that "help" comes from for a single-phase AC motor to get going in one direction can vary. Usually, it comes from an additional set of windings positioned differently from the main set, and energized with an AC voltage that is out of phase with the main power:
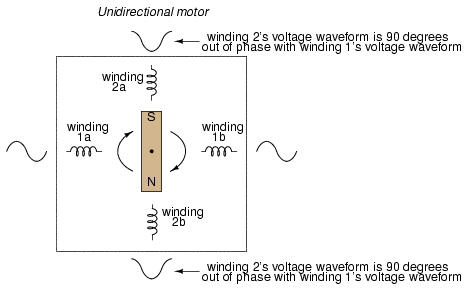
These supplementary coils are typically connected in series with a capacitor to introduce a phase shift in current between the two sets of windings:
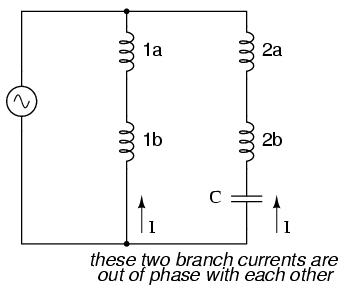
That phase shift creates magnetic fields from coils 2a and 2b that are equally out of step with the fields from coils 1a and 1b. The result is a set of magnetic fields with a definite phase rotation. It is this phase rotation that pulls the rotating magnet around in a definite direction.
Polyphase AC motors require no such trickery to spin in a definite direction. Because their supply voltage waveforms already have a definite rotation sequence, so do the respective magnetic fields generated by the motor's stationary windings. In fact, the combination of all three phase winding sets working together creates what is often called a rotating magnetic field. It was this concept of a rotating magnetic field that inspired Nikola Tesla to design the world's first polyphase electrical systems (simply to make simpler, more efficient motors). The line current and safety advantages of polyphase power over single phase power were discovered later.
What can be a confusing concept is made much clearer through analogy. Have you ever seen a row of blinking light bulbs such as the kind used in Christmas decorations? Some strings appear to "move" in a definite direction as the bulbs alternately glow and darken in sequence. Other strings just blink on and off with no apparent motion. What makes the difference between the two types of bulb strings? Answer: phase shift!
Examine a string of lights where every other bulb is lit at any given time:
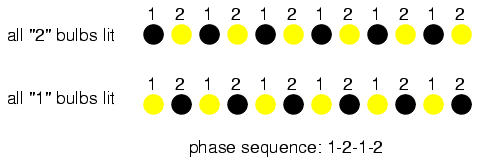
When all of the "1" bulbs are lit, the "2" bulbs are dark, and visa-versa. With this blinking sequence, there is no definite "motion" to the bulbs' light. Your eyes could follow a "motion" from left to right just as easily as from right to left. Technically, the "1" and "2" bulb blinking sequences are 180o out of phase (exactly opposite each other). This is analogous to the single-phase AC motor, which can run just as easily in either direction, but which cannot start on its own because its magnetic field alternation lacks a definite "rotation."
Now let's examine a string of lights where there are three sets of bulbs to be sequenced instead of just two, and these three sets are equally out of phase with each other:
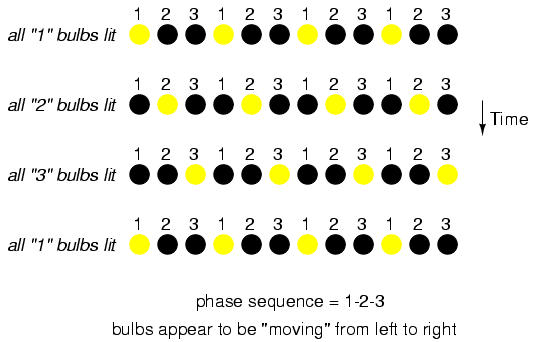
If the lighting sequence is 1-2-3 (the sequence shown), the bulbs will appear to "move" from left to right. Now imagine this blinking string of bulbs arranged into a circle:
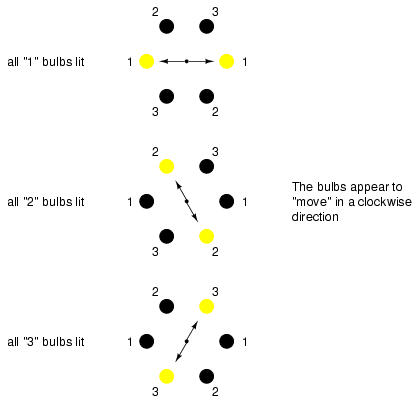
Now the lights appear to be "moving" in a clockwise direction because they are arranged around a circle instead of a straight line. It should come as no surprise that the appearance of motion will reverse if the phase sequence of the bulbs is reversed.
The blinking pattern will either appear to move clockwise or counter-clockwise depending on the phase sequence. This is analogous to a three-phase AC motor with three sets of windings energized by voltage sources of three different phase shifts:

With phase shifts of less than 180o we get true rotation of the magnetic field. With single-phase motors, the rotating magnetic field necessary for self-starting must to be created by way of capacitive phase shift. With polyphase motors, the necessary phase shifts are there already. Plus, the direction of shaft rotation for polyphase motors is very easily reversed: just swap any two "hot" wires going to the motor, and it will run in the opposite direction!
Initially we explored the idea of three-phase power systems by connecting three voltage sources together in what is commonly known as the "Y" (or "star") configuration. This configuration of voltage sources is characterized by a common connection point joining one side of each source:
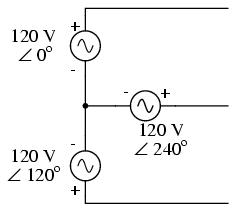
If we draw a circuit showing each voltage source to be a coil of wire (alternator or transformer winding) and do some slight rearranging, the "Y" configuration becomes more obvious:
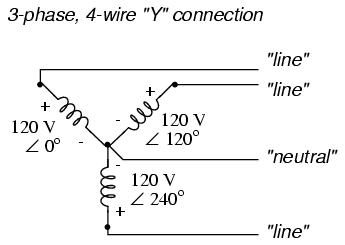
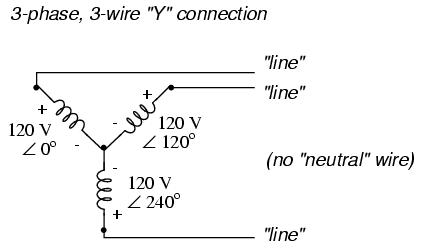
The three conductors leading away from the voltage sources (windings) toward a load are typically called lines, while the windings themselves are typically called phases. In a Y-connected system, there may or may not be a neutral wire attached at the junction point in the middle, although it certainly helps alleviate potential problems should one element of a three-phase load fail open, as discussed earlier:
When we measure voltage and current in three-phase systems, we need to be specific as to where we're measuring. Line voltage refers to the amount of voltage measured between any two line conductors in a balanced three-phase system. With the above circuit, the line voltage is roughly 208 volts. Phase voltage refers to the voltage measured across any one component (source winding or load impedance) in a balanced three-phase source or load. For the circuit shown above, the phase voltage is 120 volts. The terms line current and phase current follow the same logic: the former referring to current through any one line conductor, and the latter to current through any one component.
Y-connected sources and loads always have line voltages greater than phase voltages, and line currents equal to phase currents. If the Y-connected source or load is balanced, the line voltage will be equal to the phase voltage times the square root of 3:
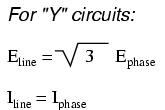
However, the "Y" configuration is not the only valid one for connecting three-phase voltage source or load elements together. Another configuration is known as the "Delta," for its geometric resemblance to the Greek letter of the same name (Δ). Take close notice of the polarity for each winding in the drawing below:
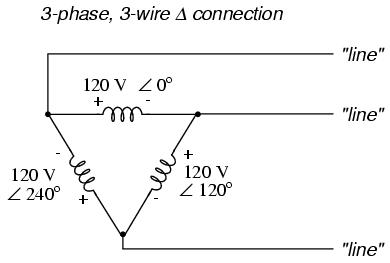
At first glance it seems as though three voltage sources like this would create a short-circuit, electrons flowing around the triangle with nothing but the internal impedance of the windings to hold them back. Due to the phase angles of these three voltage sources, however, this is not the case.
One quick check of this is to use Kirchhoff's Voltage Law to see if the three voltages around the loop add up to zero. If they do, then there will be no voltage available to push current around and around that loop, and consequently there will be no circulating current. Starting with the top winding and progressing counter-clockwise, our KVL expression looks something like this:
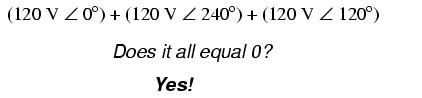
Indeed, if we add these three vector quantities together, they do add up to zero. Another way to verify the fact that these three voltage sources can be connected together in a loop without resulting in circulating currents is to open up the loop at one junction point and calculate voltage across the break:
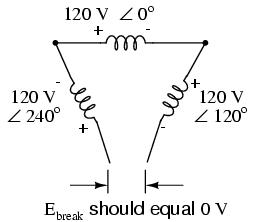
Starting with the right winding (120 V ∠ 120o) and progressing counter-clockwise, our KVL equation looks like this:
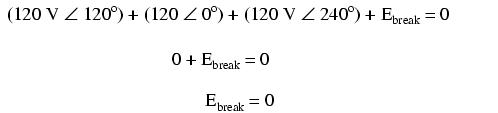
Sure enough, there will be zero voltage across the break, telling us that no current will circulate within the triangular loop of windings when that connection is made complete.
Having established that a Δ-connected three-phase voltage source will not burn itself to a crisp due to circulating currents, we turn to its practical use as a source of power in three-phase circuits. Because each pair of line conductors is connected directly across a single winding in a Δ circuit, the line voltage will be equal to the phase voltage. Conversely, because each line conductor attaches at a node between two windings, the line current will be the vector sum of the two joining phase currents. Not surprisingly, the resulting equations for a Δ configuration are as follows:

Let's see how this works in an example circuit:

With each load resistance receiving 120 volts from its respective phase winding at the source, the current in each phase of this circuit will be 83.33 amps:

So, the each line current in this three-phase power system is equal to 144.34 amps, substantially more than the line currents in the Y-connected system we looked at earlier. One might wonder if we've lost all the advantages of three-phase power here, given the fact that we have such greater conductor currents, necessitating thicker, more costly wire. The answer is no. Although this circuit would require three number 1 gage copper conductors (at 1000 feet of distance between source and load this equates to a little over 750 pounds of copper for the whole system), it is still less than the 1000+ pounds of copper required for a single-phase system delivering the same power (30 kW) at the same voltage (120 volts conductor-to-conductor).
One distinct advantage of a Δ-connected system is its lack of a neutral wire. With a Y-connected system, a neutral wire was needed in case one of the phase loads were to fail open (or be turned off), in order to keep the phase voltages at the load from changing. This is not necessary (or even possible!) in a Δ-connected circuit. With each load phase element directly connected across a respective source phase winding, the phase voltage will be constant regardless of open failures in the load elements.
Perhaps the greatest advantage of the Δ-connected source is its fault tolerance. It is possible for one of the windings in a Δ-connected three-phase source to fail open without affecting load voltage or current!
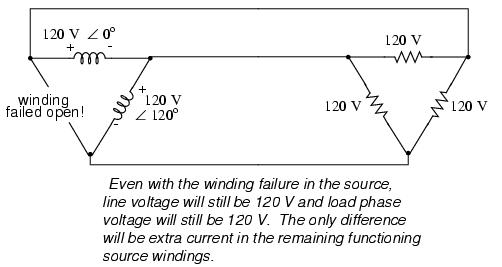
The only consequence of a source winding failing open for a Δ-connected source is increased phase current in the remaining windings. Compare this fault tolerance with a Y-connected system suffering an open source winding:

With a Δ-connected load, two of the resistances suffer reduced voltage while one remains at the original line voltage, 208. A Y-connected load suffers an even worse fate with the same winding failure in a Y-connected source:

In this case, two load resistances suffer reduced voltage while the third loses supply voltage completely! For this reason, Δ-connected sources are preferred for reliability. However, if dual voltages are needed (e.g. 120/208) or preferred for lower line currents, Y-connected systems are the configuration of choice.
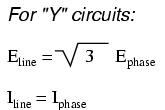

Since three-phase is used so often for power distribution systems, it makes sense that we would need three-phase transformers to be able to step voltages up or down. This is only partially true, as regular single-phase transformers can be ganged together to transform power between two three-phase systems in a variety of configurations, eliminating the requirement for a special three-phase transformer. However, special three-phase transformers are built for those tasks, and are able to perform with less material requirement, less size, and less weight from their modular counterparts.
A three-phase transformer is made of three sets of primary and secondary windings, each set wound around one leg of an iron core assembly. Essentially it looks like three single-phase transformers sharing a joined core:
Those sets of primary and secondary windings will be connected in either Δ or Y configurations to form a complete unit. The various combinations of ways that these windings can be connected together in will be the focus of this section.
Whether the winding sets share a common core assembly or each winding pair is a separate transformer, the winding connection options are the same:
The reasons for choosing a Y or Δ configuration for transformer winding connections are the same as for any other three-phase application: Y connections provide the opportunity for multiple voltages, while Δ connections enjoy a higher level of reliability (if one winding fails open, the other two can still maintain full line voltages to the load).
Probably the most important aspect of connecting three sets of primary and secondary windings together to form a three-phase transformer bank is attention to proper winding phasing (the dots used to denote "polarity" of windings). Remember the proper phase relationships between the phase windings of Δ and Y:
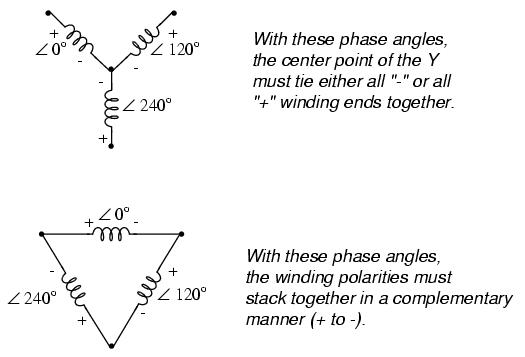
Getting this phasing correct when the windings aren't shown in regular Y or Δ configuration can be tricky. Let me illustrate:
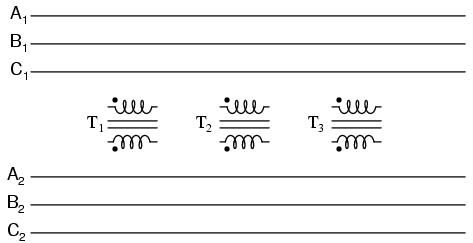
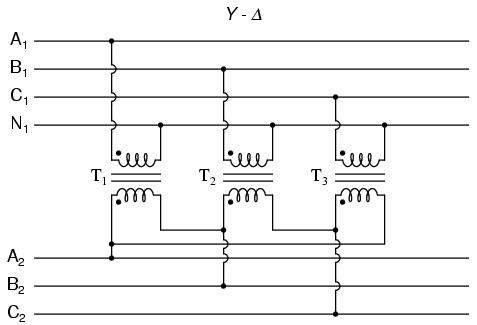
Three individual transformers are to be connected together to transform power from one three-phase system to another. First, I'll show the wiring connections for a Y-Y configuration:

Note how all the winding ends marked with dots are connected to their respective phases A, B, and C, while the non-dot ends are connected together to form the centers of each "Y". Having both primary and secondary winding sets connected in "Y" formations allows for the use of neutral conductors (N1 and N2) in each power system.
Now, we'll take a look at a Y-Δ configuration:
Note how the secondary windings (bottom set) are connected in a chain, the "dot'" side of one winding connected to the "non-dot" side of the next, forming the Δ loop. At every connection point between pairs of windings, a connection is made to a line of the second power system (A, B, and C).
Now, let's examine a Δ-Y system:
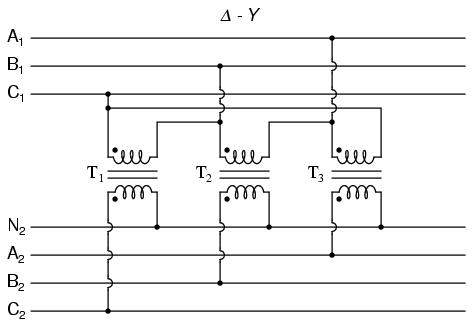
Such a configuration would allow for the provision of multiple voltages (line-to-line or line-to-neutral) in the second power system, from a source power system having no neutral.
And finally, we turn to the Δ-Δ configuration:
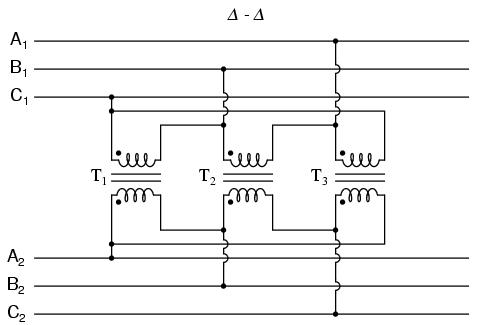
When there is no need for a neutral conductor in the secondary power system, Δ-Δ connection schemes are preferred because of the inherent reliability of the Δ configuration.
Considering that a Δ configuration can operate satisfactorily missing one winding, some power system designers choose to create a three-phase transformer bank with only two transformers, representing a Δ-Δ configuration with a missing winding in both the primary and secondary sides:
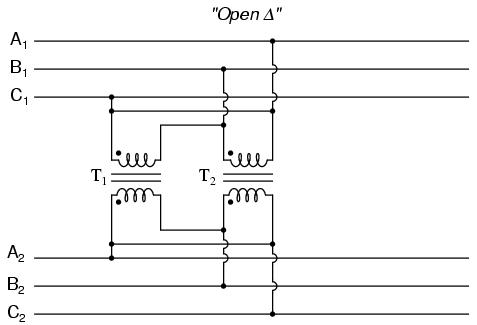
This configuration is called "V" or "Open-Δ." Of course, each of the two transformers have to be oversized to handle the same amount of power as three in a standard Δ configuration, but the overall size, weight, and cost advantages are often worth it. Bear in mind, however, that with one winding set missing from the Δ shape, this system no longer provides the fault tolerance of a normal Δ-Δ system. If one of the two transformers were to fail, the load voltage and current would definitely be affected.
The following photograph shows a bank of step-up transformers at the Grand Coulee hydroelectric dam in Washington state. Several transformers (green in color) may be seen from this vantage point, and they are grouped in threes: three transformers per hydroelectric generator, wired together in some form of three-phase configuration. The photograph doesn't reveal the primary winding connections, but it appears the secondaries are connected in a Y configuration, being that there is only one large high-voltage insulator protruding from each transformer. This suggests the other side of each transformer's secondary winding is at or near ground potential, which could only be true in a Y system. The building to the left is the powerhouse, where the generators and turbines are housed. On the right, the sloping concrete wall is the downstream face of the dam:



